
In later chapters, we will see how this condition generalizes to systems of conservation laws.
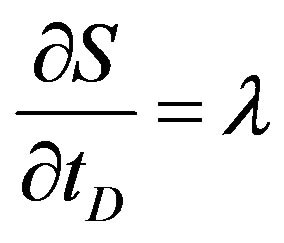
Which can be clearly observed in the interactive solution below (in the notebook). In the case of Burgers' equation, the flux function is $f(q)=q^2/2$, so the correct solution is a shock only if If nearby characteristics are spreading out, as in the last example, the correct solution is instead a rarefaction. This is often called the Lax Entropy Condition. In other words, the solution is a shock only if nearby characteristics from the left and right approach the shock as time progresses. In the case of scalar conservation laws, the entropy condition is quite simple and can be formulated in terms of the flux function of the conservation law as follows: the solution of a scalar Riemann problem will consist of a shock only if In the context of the Riemann problem, the entropy condition allows us to determine if the physical solution should involve a shock or a rarefaction. More discussion of this and several other formulations of admissibility conditions, with more detailed explanations, are available in the literature, for example in many of the books cited in the Preface. A mathematical "entropy function" with a similar property can often be defined for other conservation laws. A discontinuity that violates this is non-physical. This name comes from gas dynamics, where the physical entropy must increase in the gas passing through a shock, according to the second law of thermodynamics.
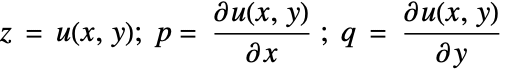
After characteristics cross, there is no strong solution of the conservation law, and we must resort to weak solutions.Ī given initial value problem for a hyperbolic PDE may have many weak solutions.Ī condition that selects a unique physically correct solution out of these weak solutions is called an admissibility condition or more often an entropy condition. The shock solution presented above, for instance, is a weak solution of Burgers' equation. Weak solutions are thus allowed to include discontinuities. Note that any weak solution is a solution of the integral conservation law and vice versa. Nonetheless, we can approximate this function arbitrarily well by a smooth function. Our study of the dynamics of equation (\ref) does not satisfy these conditions since it is not smooth. Burgers' equation is often viewed as a simplified version of equations in fluid dynamics or water waves that also have nonlinear fluxes. This equation looks very similar to the advection equation, with the difference that the advection speed at each point is given by the solution $q$. The quasilinear form is obtained by applying the chain rule to the flux term: Burgers' equation is a scalar conservation law with flux $f(q)=q^2/2$: doi:10.1137/1.9781611970562.Burgers' equation has been used extensively for developing both theory and numerical methods, and it will allow us to explore the Riemann problem for a nonlinear conservation law. Lax, Hyperbolic systems of conservation laws and the mathematical theory of shock waves. $x$, one has $u_x = q_0/(1+q_0 k y)$ with the same notations as above. The implicit equation $u = h(x-a(u) y)$ can be solved for $u$ as a differentiable function of $x$ and $y$ for $y$ small enough. We differentiate the PDE with respect to $x$, and we set $q=u_x$, $q' = q_y + a(u) q_x$. The smallest such $y$ is the breaking time. This derivative vanishes at $y = -1/(a\circ h)'(x_0)$. We differentiate the expression of characteristics $x = x_0 + a\circ h(x_0)\, y$ with respect to the initial abscissa $x_0$. (1)), which is based on the intersection of characteristics and the mean value theorem.

There are several other proofs than the previous geometric argument (cf. This is the $y$ where a shock wave occurs ( breaking time). The initial curve $\Gamma : $ and the characteristic differential equations are $\frac\. Show that the solution becomes singular for some positive $y$, unless $a(h(s))$ is a nondecreasing function of $s$ With initial condition $u(x,0)=h(x)$ is given implicitly by Show that the solution $u$ of the quasi-linear PDE:


 0 kommentar(er)
0 kommentar(er)
